Z-scores & Probability

Lecture 7

Dave Brocker

Farmingdale State College

Review

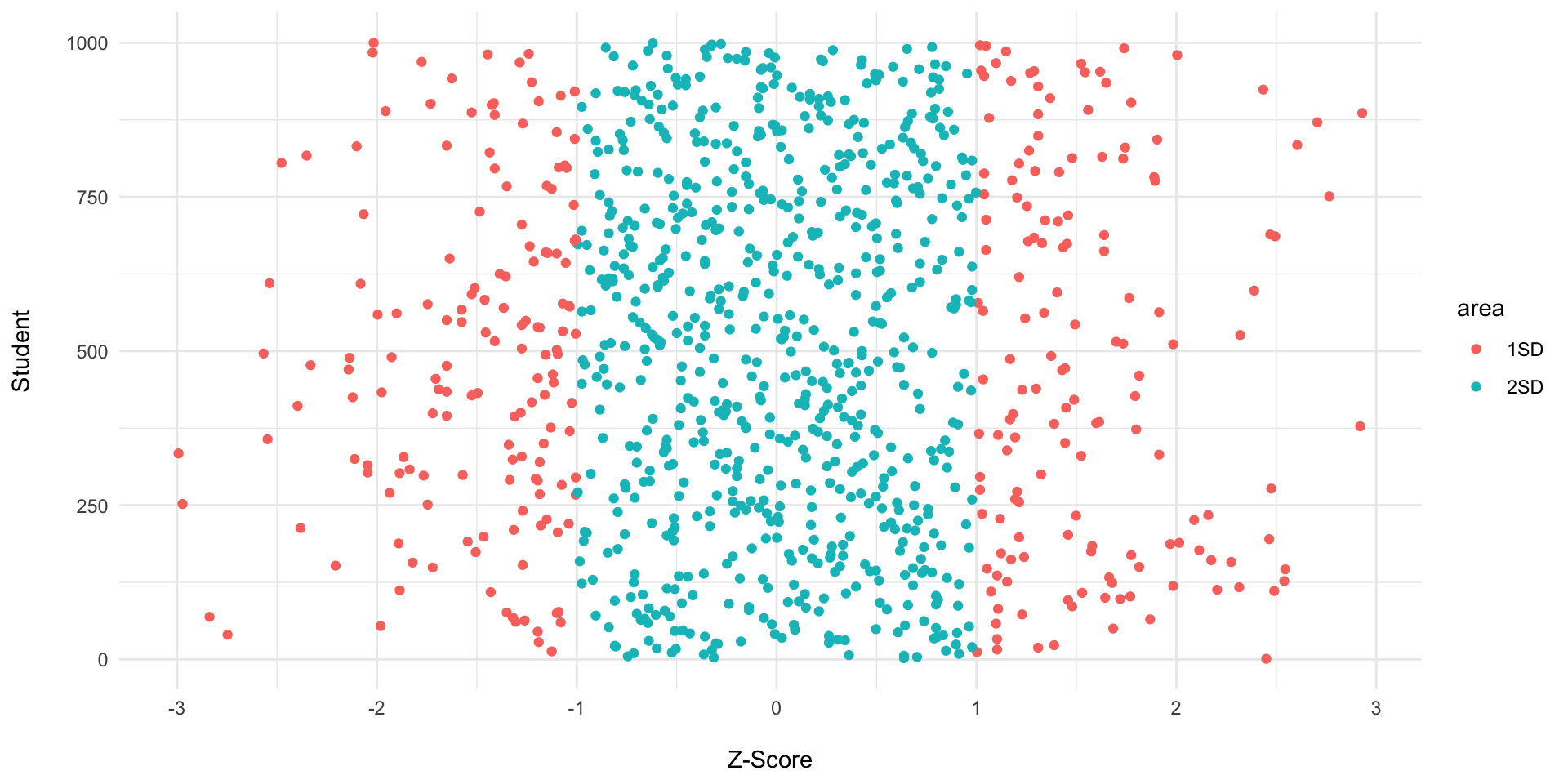
Proportional Breakdown

  • 68.3% of the datapoints (the X’s) will fall within 1 SD of the mean.

  • 95.4% of the datapoints (the X’s) will fall within 2 SD of the mean.

  • 99.7% of the datapoints (the X’s) will fall within 3 SD of the mean.

Z-scores are expressed in Standard Deviation units.

Z-scores

Why do we care?

Z-scores re-express the original data points (the X’s) in a way that intuitively lets us know:

  • How close the X is to the mean

  • Where it falls in the dispersion of the distribution

  • How much this participant is like the other person in the sample

Z-scores

Why do we care?

Z-scores re-express the original data points (the X’s) in a way that intuitively lets us know:

  • Where it falls in the dispersion of the distribution

  • How different this participant is from the majority of people in the sample

Z-scores

Why do we care?

Z-scores

Why do we care?

Z-scores

Imagine that \(s\) = 2 and \(\bar{x}\) = 25

Z-scores are expressed in Standard Deviation units.

  • \[z = 1 = 25 + 2 = 27\]

  • \[z = -2 = 25 - 2 = 23\]

  • \[z = 0.5 = 25 - .05 = 24.4\]

Calculating A Z-score

Step-by-Step

  • Mean-center the X values \(x - \bar{x}\)

    • This makes the Mean = 0.

  • Dividing by the standard deviation \(\frac{}{s}\)

    • Makes the SD = 1.

Calculating Probability

Use the normal distribution

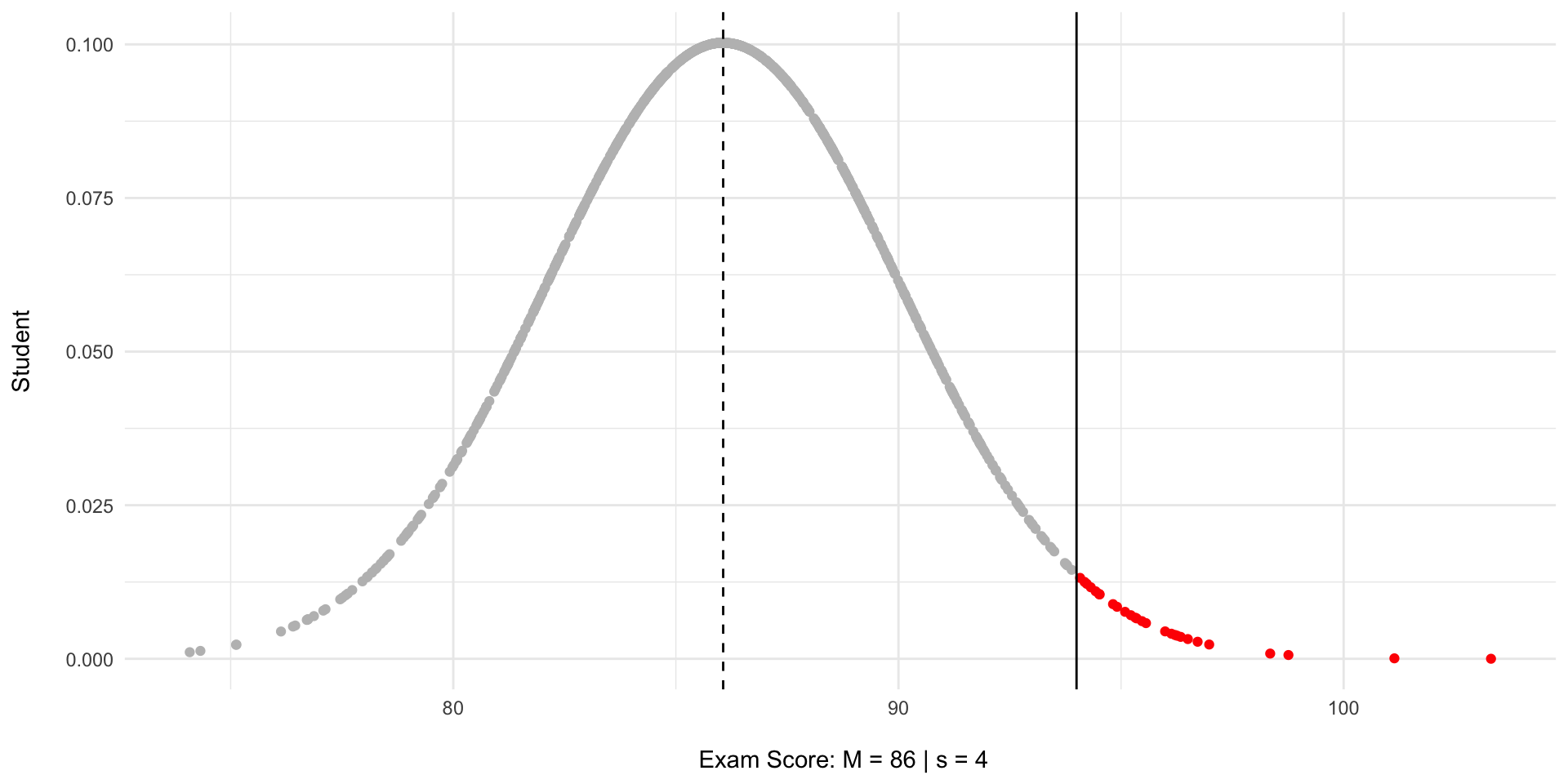
The average grade on the exam was an 86 with a standard deviation of 4.

Calculating Probability

The average grade on the exam was an 86 with a standard deviation of 4. What is the probability of scoring a 94 or higher on the exam?

Calculating Probability

Use the normal distribution

The average grade on the exam was an 86 with a standard deviation of 4. What is the probability of scoring a 94 or higher on the exam?

  • \[z = \frac{x-\bar{x}}{s} = \frac{94-86}{4} = \frac{8}{4}=2\]

  • Z = 2 corresponds with 2.1% and 0.1% of the curve (2.2%) chance.

Example 2

Test Time!

The mean exam score was 86 with a standard deviation of 4.

Example 2

Esmeralda’s Second Test

What is the probability of scoring between an 82 and a 90?

Example 2

Esmeralda’s Second Test

What is the probability of scoring between an 82 and a 90?

  • \(z = \frac{82-86}{4} = \frac{-4}{4} = -1\)

  • \(z = \frac{90-86}{4} = \frac{4}{4} = 1\)

  • There is a 68.3% chance of scoring between 82 and 90.

Example 3

Esmeralda’s Second Test

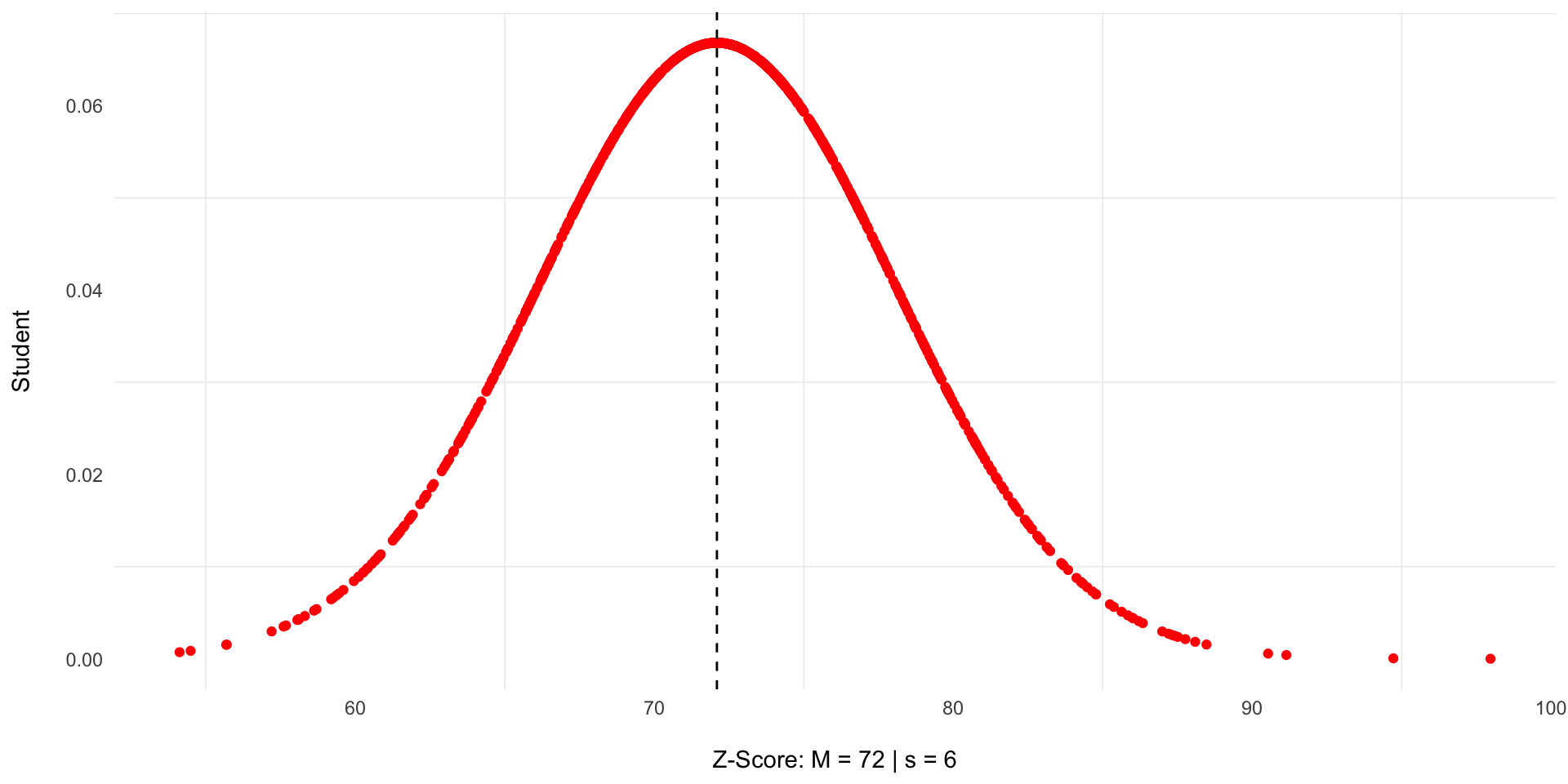
Esmeralda’s stats professor tells her class that the average score on the exam was a 72 with a standard deviation of 6, and the distribution of scores was normal.

Example 3

Esmeralda’s Second Test

Esmeralda wants to calculate the probability that she scored below 60

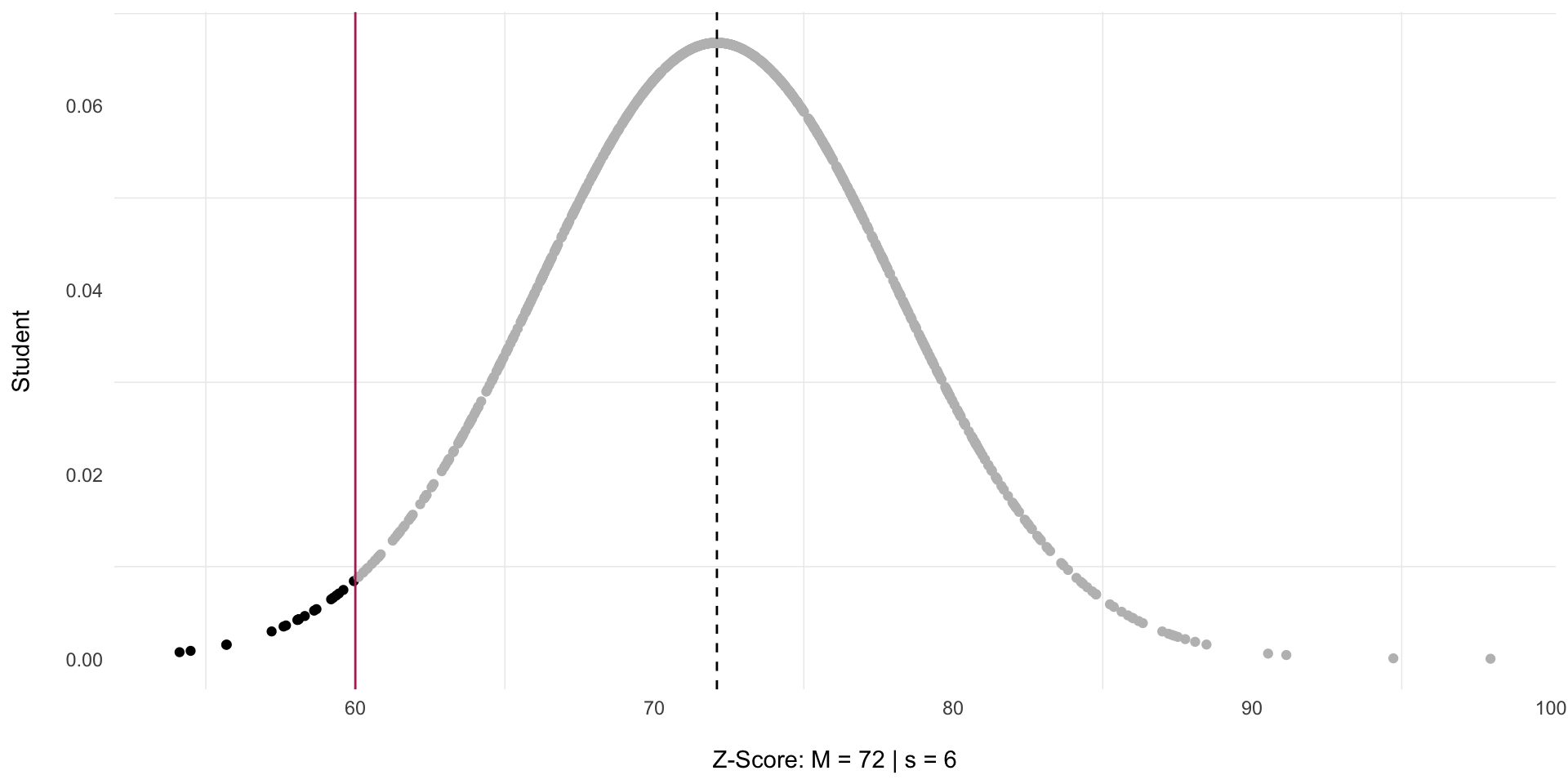
Example 3

Esmeralda’s Second Test: \(\bar{x} = 72 | s = 6\)

Esmeralda wants to calculate the probability that she scored below 60

  • \(\frac{60-72}{6} = \frac{-12}{6} = -2\)

  • 2.2% chance that she failed.

  • What’s the chance she passed?

Z-scores and Probability

How does it apply?

In real life, we are often working with numbers with long decimal points rather than nice whole numbers.

  • Because the standard normal curve is STANDARD and NORMAL, we can calculate the exact probability of a z-score with a decimal point.

  • Calculate the z-score.

Z-scores and Probability

How does it apply?

In real life, we are often working with numbers with long decimal points rather than nice whole numbers.

  • Locate the whole number and first decimal point along the left side of the table.

  • Locate the second decimal point along the top of the table.

Z-scores and Probability

The Z-score Probability Table gives you the probability of that z-score or LESS.

  • If you need that z-score or higher, you have to subtract the decimal from 1.

Z-scores and Probability:

Some examples

In a recent study on world happiness, participants were asked to evaluate their current lives on a scale from 0 to 10, where 0 represents the worst possible life and 10 represents the best possible life. The responses were normally distributed, with a mean of 5.4 and a standard deviation of 2.2. Find the probability that a randomly selected study participant’s response was:

  • Less than 4

  • More than 8

Z-scores and Probability:

Life Satisfaction: \(\bar{x} = 5.4 | s = 2.2\)

  • Find the probability that a randomly selected study participant’s response was:

  • Less than 4

  • More than 8

  • \[z = \frac{x-\bar{x}}{s} = \frac{4-5.4}{2.2} = \frac{-1.4}{2.2} = -.63\]

  • \[z = \frac{x-\bar{x}}{s} = \frac{8-5.4}{2.2} = \frac{2.6}{2.2} = 1.18\]

Z-scores and Probability

Example 1

Z-table

Example 1

Step by Step

Z-table

Z-scores and Probability:

Example 2

The scale of scores for an IQ test are approximately normal with mean 100 and standard deviation 15. The organization MENSA, which calls itself the “high IQ society”, requires a score of 130 or higher.

What percent of adults would qualify for membership?

Z-scores and Probability:

Example 2

The scale of scores for an IQ test are approximately normal with mean 100 and standard deviation 15. The organization MENSA, which calls itself the “high IQ society”, requires a score of 130 or higher.

What percent of adults would qualify for membership?

  • \(z = \frac{x-\bar{x}}{s} = z = \frac{130-100}{15}=\frac{30}{15} = 2\)

Example 2

MENSA

Z-table