Z-scores

Lecture 5

Dave Brocker

Farmingdale State College

Standard Normal Distribution

What do we know about normal distributions?

• They are shaped like a bell (“bell curve”).

• They are symmetric.

• They are unimodal.

• The mean = median = mode.

Standard Deviation

Standard deviation is in the scale of the variable (x).

• A standard deviation of 1 means a distance of 1 on the scale used to measure the variable.
• Jonas scores a 98 on the exam. The average grade on the exam was 97 with a standard deviation of 1.
  • Find Jonas’ score on the normal distribution.

Standard Deviation

Standard deviation is in the scale of the variable (x).

• Jonas scores a 98 on the exam. The average grade on the exam was 97 with a standard deviation of 1.
  • Find Jonas’ score on the normal distribution.

Standard Normal Distribution

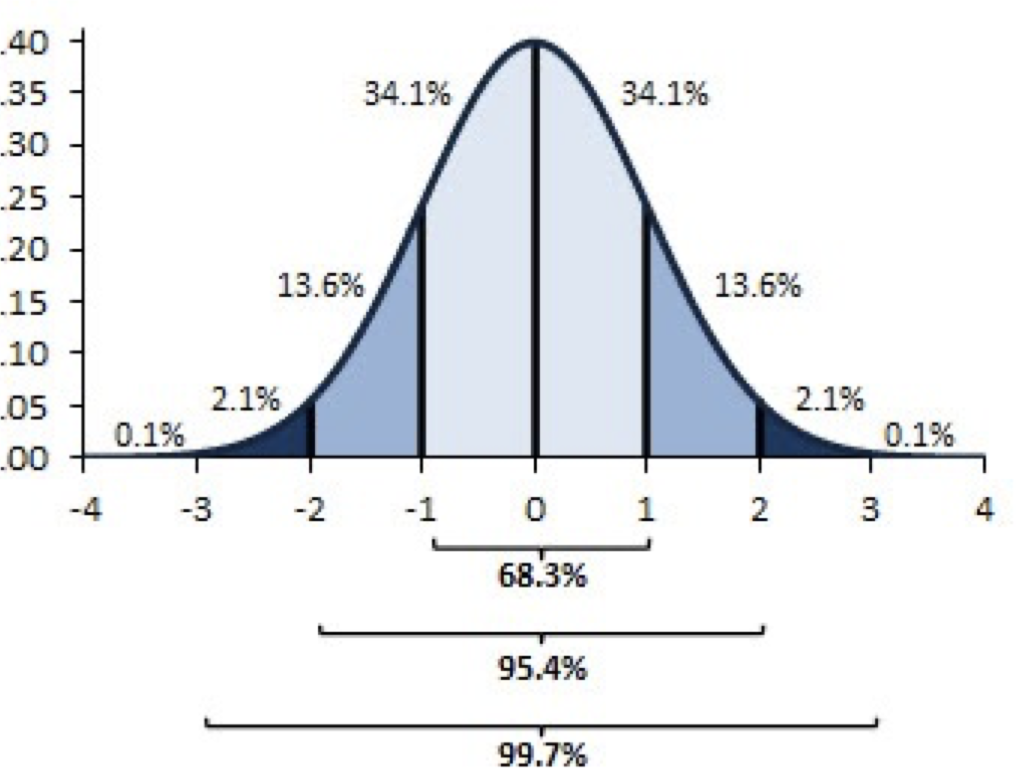
Percentages and Proportions

• 68.3% of the data will fall within 1 SD of the mean.

• 95.4% of the data will fall within 2 SD of the mean.

• 99.7% of the data will fall within 3 SD of the mean.

• “Within one standard deviation” means +1 as well as -1 standard deviation.

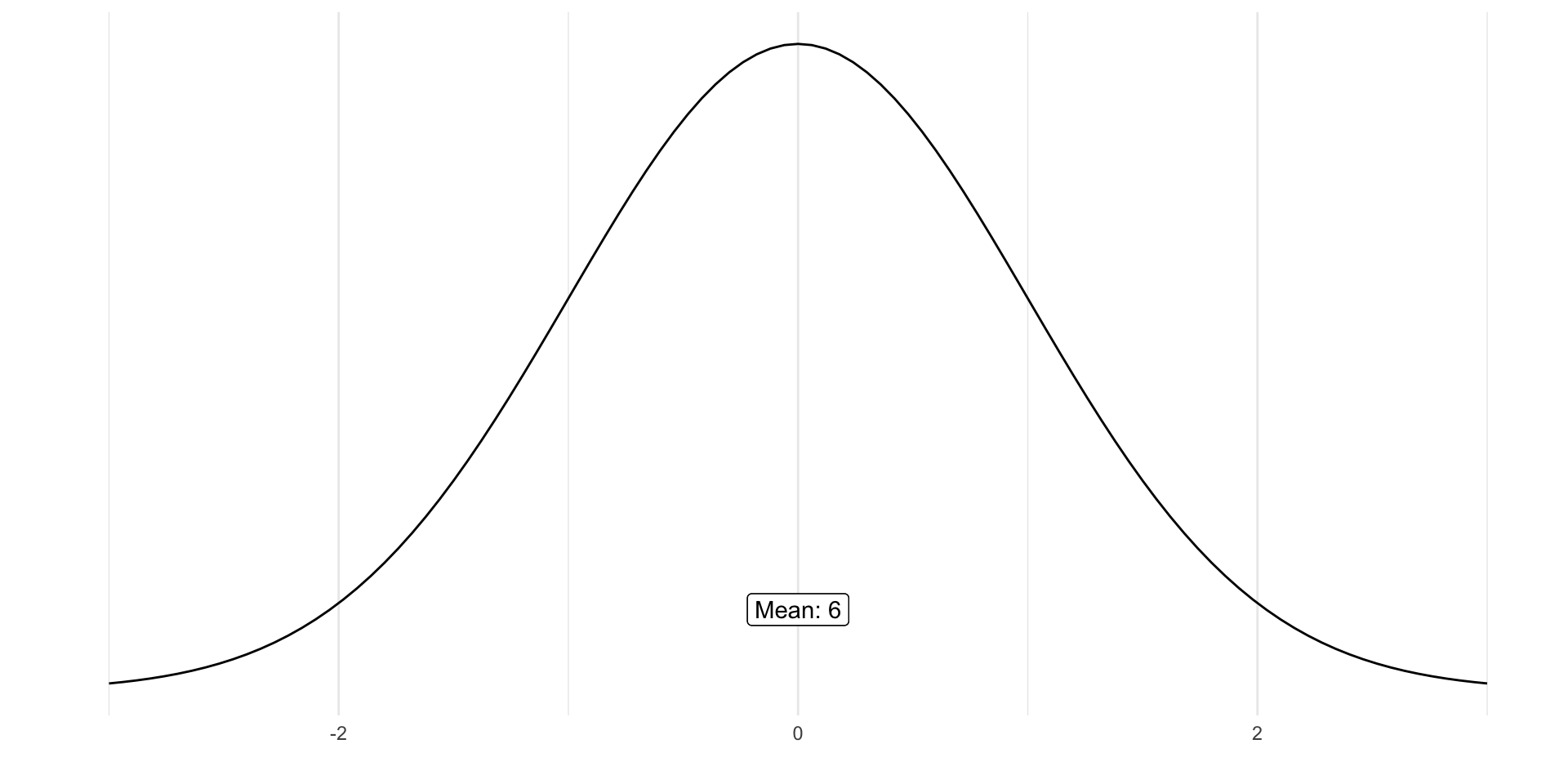
Standard Normal Distribution

Example 1

Students’ ratings of the Netflix Original Dark (range = 1- 10) form a normal distribution with m = 6 and s = 1.

• What percentage of Students rate it a 7 or higher?

• What percentage of Students rate it at least a 4?

• What percentage of Students rate it an 8 or lower?

Standard Normal Distribution

Example 1:

Students’ ratings of the Netflix Original Dark form a normal distribution with m = 6 and s = 1.

• What percentage of Students rate it a 7 or higher?

• 15.8% (13.6 [1SD] + 2.1[2SD] + .1[3SD])

Standard Normal Distribution

Example 1:

Students’ ratings of the Netflix Original Dark form a normal distribution with m = 6 and s = 1.

• What percentage of Students rate it at least a 4?

• 2.2%

Standard Normal Distribution

Example 1:

Students’ ratings of the Netflix Original Dark form a normal distribution with m = 6 and s = 1.

• What percentage of Students rate it an 8 or lower?

• 97.6%

Z-scores

What does it do?

A z-score tells you, in standard deviation units how far the x-value is from the mean.

• Z-scores are better than using raw SD

• When the SD is a decimal, it is hard to find the exact point under the standard normal curve.

Z-scores

Rule of Thumb

• The distance from the mean to the 1 on this standard normal curve is equal to the SD.
• The distance from the mean to the 1 on this standard normal curve is equal to z=1.

Z-scores:

Find: Z = 1 | Z = -2 | Z = 0.5

Z-scores

What do they do!

• Z-scores re-express the original data points (the x’s) in a way that intuitively lets us know:

• How close the x is to the mean (how much this particular participant is like the average person in the sample)

• Where it falls in the dispersion of the distribution (how different this particular participant is from the majority of people in the sample)

Calculating

Z-scores

Formula

\[ z = \large{\frac{\color{orange}{x}-\color{red}{\bar{x}}}{\color{pink}{s}}} \]

• Subtract each x value from the mean.

• Divide by the standard deviation

Practice Examples

Example 1

z = \(\frac{x - \mu}{\sigma}\)

• Mean (\(\mu\)) = 50

• Standard deviation (\(\sigma\)) = 10

• Raw score (x) = 65

• Find the z-score.

• \(\frac{65-50}{10} = 1.5\)

Practice Examples

Example 2

• Mean (\(\mu\)) = 100

• Standard deviation (\(\sigma\)) = 15

• Raw score (x) = 85

• Find the z-score.

• \(\frac{85-100}{15} = -1\)

Practice Examples

Example 3

• Mean (\(\mu\)) = 70

• Standard deviation (\(\sigma\)) = 8

• Raw score (x) = 66

• Find the z-score.

• $ = .5

Practice Examples

Example 4

• Mean (\(\mu\)) = 500

• Standard deviation (\(\sigma\)) = 120

• Raw score (x) = 740

• Find the z-score.

• \(\frac{740-500}{120} = 2\)

Practice Examples

Example 5

• Mean (\(\mu\)) = 40

• Standard deviation (\(\sigma\)) = 6

• z-score = +2.5

• Find the raw score (x).

• \(2.5 = \frac{x-40}{6}\)

• \(x = z\times s = 2.5\times6=15\)

Z-scores

Z-Scores are calculated by

• Centering the X values on the mean: When we center the mean (mean-centering), we set the mean to 0.

• Dividing by the standard deviation

• When we divide by the SD, the space from the mean is expressed in standard deviations.

Z-scores

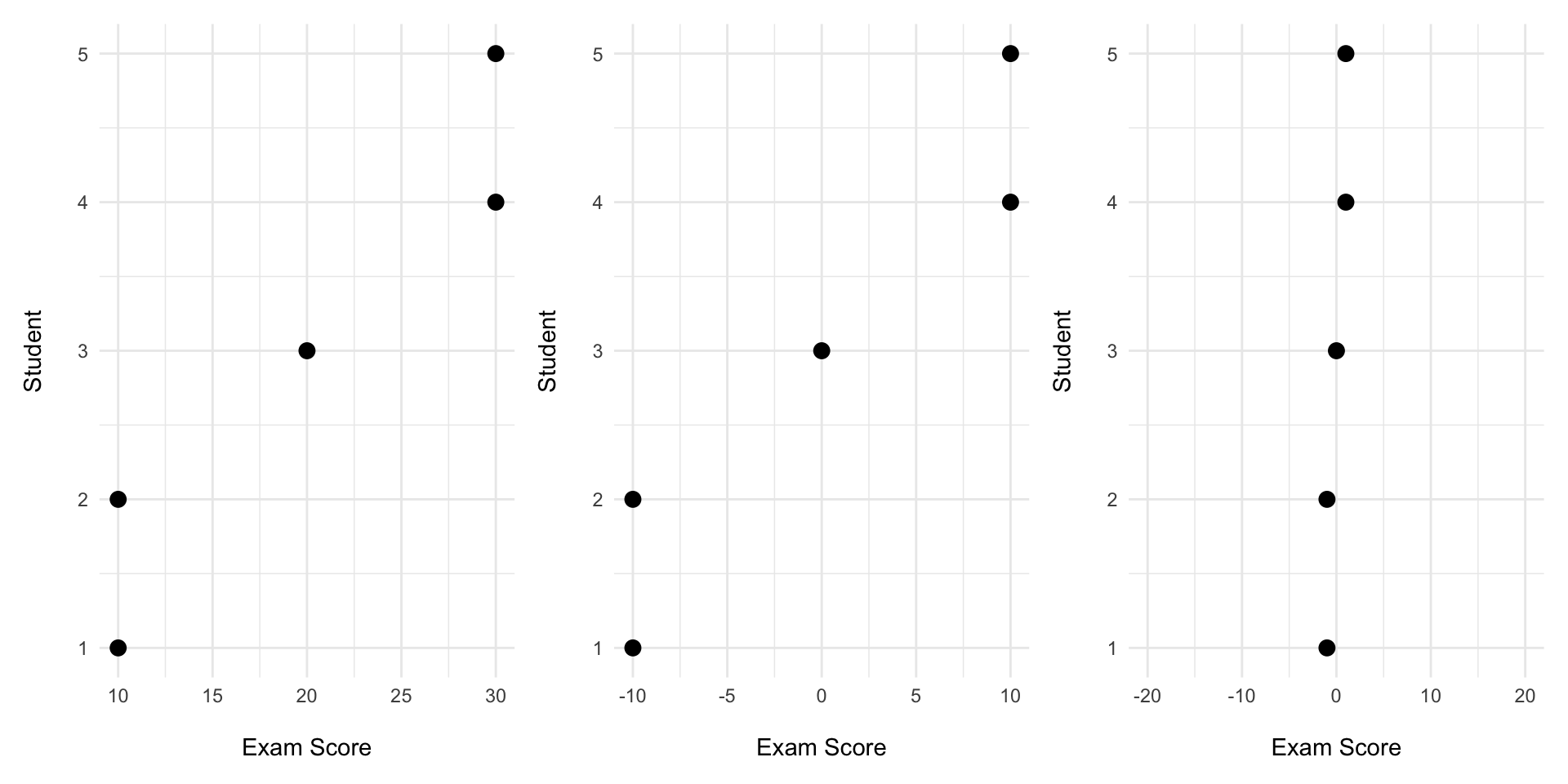
A Familiar Face: \(\bar{x} = 20\)

\(x\)	\(\bar{x}\)	\(x-\bar{x}\)	\((x-\bar{x})^2\)
10	20	−10	100
10	20	−10	100
20	20	0	0
30	20	10	100
30	20	10	100

Z-scores

Formula in Action

Average

\[\color{red}{\bar{x}} = \frac{\sum{x}}{n}\]

Standard Deviation

\[s^2 = \sqrt{\frac{\sum(x-\color{red}{\bar{x}})^2}{n-1}} = \frac{400}{4} = \sqrt{100} = s\]

Z-Score

\[z =\frac{x-\color{red}{\bar{x}}}{s} = \frac{20-10}{s}=\frac{-10}{s}\]

Z-scores

\(x\)	\(x-\bar{x}\)	\((x-\bar{x})^2\)	\(z=\frac{(x-\bar{x})^2}{s}\)
10	−10	100	−1
10	−10	100	−1
20	0	0	0
30	10	100	1
30	10	100	1

• We made the mean = 0: When you mean-center a distribution, you shift it along the number line.

• We made the SD = 1: When you divide a distribution by the SD, you shrink the distribution down.

• The shape of the distribution remains the same.

Z-scores

• Shift distribution along the number line.

• Shrink distribution down.

• The shape of the distribution remains the same.

Z-Scores

Why Do We Care?

• A z-score tells me where my score falls in SD units.

• I can then look at this standard normal curve, and estimate what percentage of people did better or worse than me.

Z-Scores

Why Do We Care?

The mean score for Exam 1 was a 92 with a standard deviation of 3.

• Esmeralda scored an 86.

• What percent of the class scored better than Esmeralda?

• \(z=\frac{x-\bar{x}}{s} = \frac{86-92}{3} = -2\)

• 98% of the class did better than Esmeralda.

Z-Scores

The mean score for Exam 1 was a 92 with a standard deviation of 3.

• Jonas scored a 95.

• What percent of the class scored better than Jonas?

• \(z = \frac{95-92}{3} = 1\)

• 16% scored higher than Jonas.

NULL