Scales of Measurement and Measures of Central Tendency

PSY 348: Lecture 3

Dave Brocker

Farmingdale State College

Studying Psychology

What do researchers in the areas of psychology that are interesting to you study?

  • Attitudes

  • Beliefs

  • Behaviors

  • Physiology

  • Planning

  • Brain Activity

  • Thoughts

  • Performance/Ability

  • Attenton

  • Memory

Measures of Central Tendency

Studying Psychology

The Bobo Doll Experiment (Bandura, 1961)

Studying Psychology

Defining Variables

  • Operationalization

    • The process of defining the measurement of a phenomenon that is not directly measurable (AKA a latent variable) though its existence is implied by other phenomena.

How could we measure happiness?

mood

Operationalization

Figuring out how to measure something you can’t directly measure.

  • Attitudes

  • Beliefs

  • Thoughts

  • Behaviors

  • Brain activity

  • Performance/Abilities

What if I wanted to measure disgust?

Operationalization

Types of Measurements

  • Self-Report or Behavioral Measures

  • Observation

  • Implicit Measures

  • Tests

Types of Measurements

Self-report

  • Surveys

  • Questionnaires

  • Polls

  • Quizzes

  • Instruments

Self-Report

What’s wrong with this?

Self-Report:

Advantages

  • Most popular method of assessing attitudes

  • Can obtain large amounts of data

    • (Fairly) Quick

  • Allows for adaptive testing

    • (Fairly) Inexpensive

Self-Report:

Disadvantages

  • Acquiescence

    • Tendency to say yes, true, agree

  • Social desirability

    • Tendency to respond in ways that are seen as socially acceptable

  • Demand characteristics

    • Tendency to response in ways that participant thinks researcher wants

Self-Report:

Avoiding Disadvantages

  • Anonymous respondents are less likely to make things up

    • Assure anonymity

  • Allow respondents to answer in private

    • Allow for maximum privacy

  • Don’t make your experiment too obvious/revealing

    • Obscure the true goal of the experiment

  • Add questions that test for respondent awareness

    • Include attention checks

  • Purposely make some questions opposite

    • Reverse coding

Behavioral Measures

Examples

  • Taking a flier

  • Signing a petition

  • Internet Behavior

  • Moving a chair

  • Donating money

Observation

The Bobo Doll Experiment (Bandura, 1961)

The Bobo Doll Experiment

(Bandura, 1961)

  • Live aggression by adult

  • Videotaped aggression by adult

  • Cartoon aggression

    • No aggression

Observation

Disadvantages

  • Time consuming

  • Different reviewers/observers may score behaviors differently.

    • Coding scheme

      • Who decides what is an example of the behavior?

    • Inter-rater Reliability

      • How much agreement is there between 2+ observers?

Implicit measures

Brain activity

  • Functional Magnetic Resonance Imaging (fMRI)

    • Neuroimaging of brain activity

  • Electroencephalography (EEG)

    • Electrodes on surface of scalp measures brain activity

Issues with Operationalization

Why is it hard to measure psychological phenomena?

  • Others may choose to measure the phenomena differently from us

  • Operationalization can be culture-specific

  • What we measure is based on observable parts of the phenomena, but some parts may not be able to be observed

    • Measuring only the observable is imprecise

How else could Bandura have measured aggression?

Operationalization

How should we measure aggression in children?

  • Observe children for one hour and…

    • Label them as Aggressive or Non-Aggressive

    • Rank them from most aggressive to least aggressive

    • Score them on a 10-point scale.

      • 1 = No Aggression

      • 10 = All of the Aggression

    • Count number of aggressive behaviors

Scales of measurement

A Scale By Any Other Name

  • Labels Nominal

  • Rank Order

  • Scale Interval

  • Count Ratio

Nominal (Categories, No Order)

  • Type of therapy (CBT, psychoanalysis, EMDR)
  • Diagnosis (Major Depressive Disorder, Generalized Anxiety Disorder, none)
  • Relationship status (single, dating, married, divorced)
  • Coffee drinker vs. non-coffee drinker

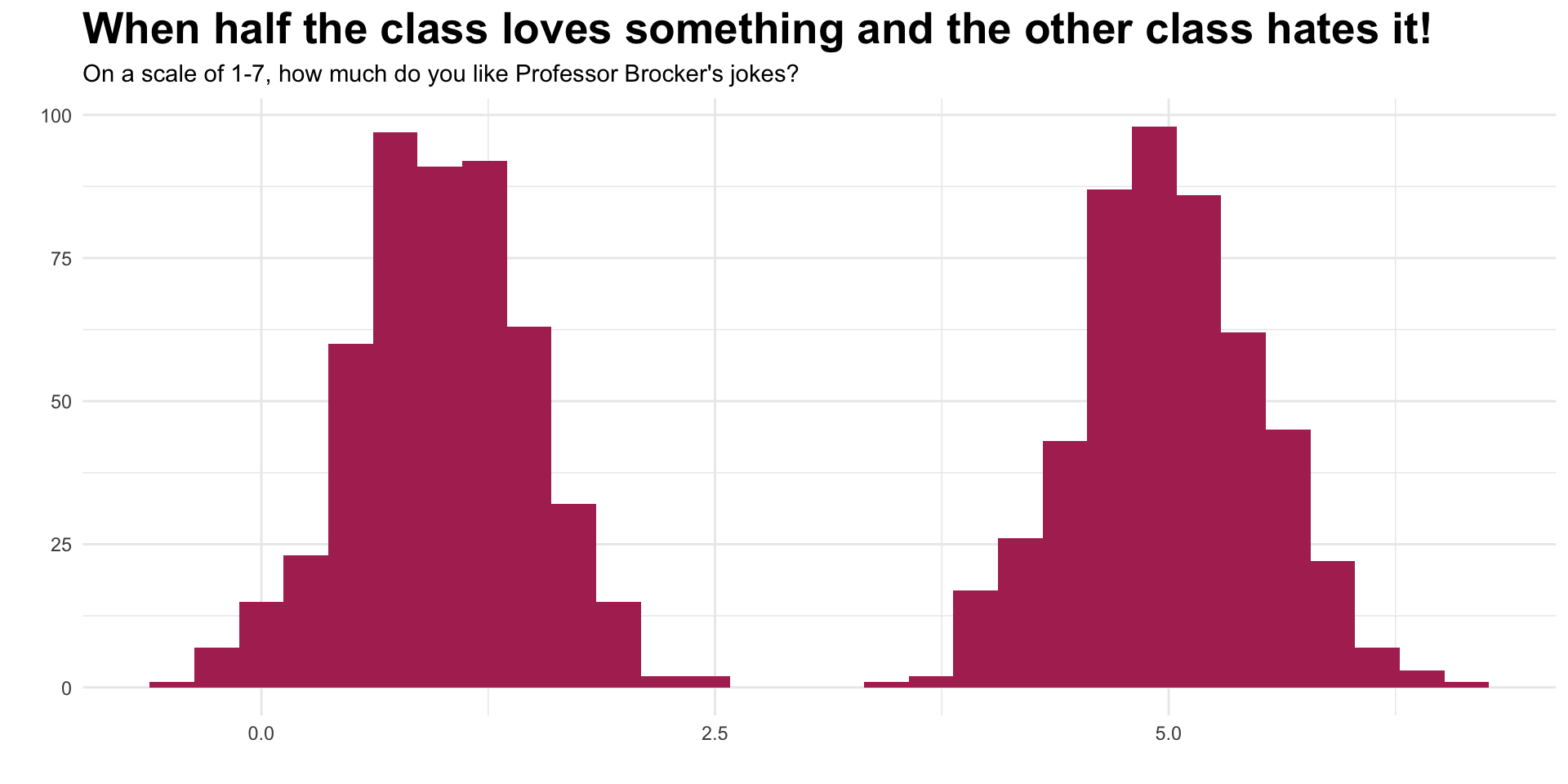
Raise your hand if you’re a coffee drinker, tea drinker, or energy-drink person. That’s nominal data.

Ordinal (Ranked, Uneven Gaps)

Examples:

  • Rank order of stress: mild / moderate / severe
  • Olympic medals (gold, silver, bronze)
  • Likert-style agreement (Strongly Disagree → Strongly Agree) — though technically often treated as interval in practice
  • Clinical severity ratings (minimal, mild, moderate, severe depression)

Who’s seen the movie Inside Out? Imagine ranking the emotions in order of how often you feel them—Fear first, then Joy, then Anger. That’s ordinal.

Interval (equal distances, no true zero)

Examples:

  • IQ scores

  • Standardized test scores (e.g., SAT, GRE)

  • Temperature in Fahrenheit or Celsius

  • GPA

If someone has a GPA of 0.0, does that mean they don’t exist as a student? No—it just means they failed. That’s why GPA is interval, not ratio.

Ratio (equal distances, true zero)

Examples:

  • Reaction time (can be 0 ms)

  • Number of therapy sessions attended

  • Cortisol level in blood

  • Hours of sleep last night

  • Money donated to a cause

How many hours of sleep did you get last night? If you got 0, that really means 0. Ratio scale.

Interval vs Ratio

What’s the difference between interval and ratio?

  • Interval may have a 0 on the scale, but it doesn’t mean the absence of something. A 0.0 GPA means an F rather than the absence of a grade.

  • Ratio has a 0 that. means 0 (the absence of something), like a ‘0’ as a response to the questions, “How many drinks did you have last night?”

Discrete and Continuous

What’s the Difference?

Discrete and Continuous

Discrete variables have predefined values

  • Number of siblings (you can’t have 2.5 siblings)

  • Number of errors on a test

  • Types of therapy (CBT, psychoanalysis, none)

  • Diagnostic category (depression, anxiety, bipolar, etc.)

  • Eye color

  • Number of cups of coffee consumed today

Discrete and Continuous

Continuous Variables can occupy several different values

  • Reaction time (seconds, milliseconds)

  • Height (inches, centimeters)

  • Weight (pounds, kilograms)

  • Self-esteem score on a 1–10 scale

  • GPA

  • Hours of sleep last night (can be 7.25 hours)

  • Brain activity (EEG voltage, fMRI signal intensity)

Determining Scale of measurement

Identify the scale of measurement.

Undergraduates report their self-esteem on a scale of 1 to 10. Researchers assess the relationship of undergraduates’ self-esteem and GPA.

  • Predictor variable: Self-Esteem | Continuous (Interval)

  • Outcome variable: GPA | Continuous (Interval)

Determining Scale of measurement

Identify the scale of measurement.

Participants are given a mystery drug or placebo and then asked to complete puzzle tasks. Researchers time how long participants take to complete the puzzles.

  • Independent variable: Drug vs. Placebo | Categorical (Nominal)

  • Dependent variable: Reaction Time | Continuous (Ratio)

Determining Scale of measurement

Identify the scale of measurement.

Undergraduates are shown either pictures of death or pictures of landscapes. They then report their anxiety about aging on a scale of 1 (none) to 10 (lots).

  • Independent variable: Pictures of death versus landscapes | Categorical (Nominal)

  • Dependent variable: Anxiety about dying | Continuous (Interval)

Why does scale of measurement matter?

For Science!

  • Statistical tests can only be run on specific scales of measurement.

  • t-test & ANOVA: Nominal IV/predictor and Continuous DV/outcome

  • Correlation & Regression: All continuous

Why does scale of measurement matter?

  • Generally, continuous variables (interval and ratio scales) lend themselves better to statistical analysis.

  • As a researcher, you should plan out your statistical analysis BEFORE conducting your study, so that you measure your variables in a way that matches the type of analyses you will run.

Takeaway: How we measure variables matters…

because it dictates what kind of statistical analyses we can run.

  • Data can be coerced into different formats

  • ‘Correct’ or ‘Supporting’ results can come from bogus data

  • We’ve measured aggression/self-esteem/attention. Now, how do we summarize all these numbers?

Statistical Terms & Symbols

Statistical Symbols

Case-sensitive and often Greek

  • \(n\) = the number of people in the sample

  • \(x\) = one datapoint in a sample

  • \(\bar{x}\) = Arithmetic mean (average) for a sample, x

  • \(\Sigma(x)\) = The sum of all values in a sample, x

  • \(\sum^{n}_{i = 1}= x_1 +x_2+x_3...\)

Practice 1

Study Up!

Esmeralda is taking Statistics for the Psychological Sciences. On her first exam, she scored 98. The average grade among the 26 students on that exam was 97

  • n:

  • x:

  • \(\bar{x}\):

Practice 2

Have you ever heard of this show?

Dave is interested in how many FSC students watch the Netflix Original, Dark. He plans to ask 200 students if they have seen it or not.

N:

n:

Scale of Measurement:

Practice 3

Be Kind to Yourself!

A research study surveys 500 college student across 5 campuses in the United States, asking them to rate their self-esteem on a scale of 1 to 10.

Sample:

Population:

Scale of Measurement:

Measures of Central Tendency

Part 2: What’s in the Middle?

Review

Scales of Measurement

  • What are the 4 scales of measurement

  • What are the only scales of measurement that matter for us?

Review

Scales of Measurement

  • Nominal

    • Categories, No Equal Gaps

  • Ordinal

    • Ordered, No Equal Gaps

  • Interval

    • Quantitative, Equal Gaps, No True 0

  • Ratio

    • Quantitative, Equal Gaps, True 0

Review

Statistical Terms

  • n = ?

  • x = ?

  • \(\bar{x}\) = ?

Review

Statistical Terms

  • n = the number of people in the sample

  • x = one participant’s score

  • \(\bar{x}\) = sample mean (pronounced x-bar)

Review

Statistical Terms

  • What is a parameter?

    • Information that describes the population.

  • What is a statistic?

    • Information that describes the sample.

    • Inferences about the population based on information from the sample.

Descriptive Statistics

Describe the characteristics of the sample.

  • Think about our data on time spent on Instagram/phones in general.

  • How could we describe it?

    • Average

      • Overall, what is the typical duration

    • Min & Max

      • Highest and Lowest

    • Most Frequent/Most Infrequent

      • What are the most common durations?

      • Least common?

Descriptive Statistics

Describe the characteristics of a sample in terms of:

  • Central tendency: What most people said (mean, median, and mode)

  • Dispersion: How spread out the data are (standard deviation)

Measures of Central tendency

  • Tell us about the mid-point (center) of a distribution.

  • Tell us about the mid-point (center) of a distribution.

  • Tell us most participants’ answer.

The average GPA in the class is 3.2

What does that actually mean?

Measures of Central tendency

Mean | Average

Important

  • The average; obtained by summing all values and dividing by the number of values.

  • \(\large{\sum^{n}_{i=1} = x_1 + x_2...}\)

  • \(\large{\frac{\sum(x)}{n}}\)

  • \(\large{[3,4,5,2,1] = \frac{\sum(3+4+5+2+1)}{5} = \frac{15}{5} = \bar{x} = 3}\)

  • Think about how you calculate your GPA or grade for a class

  • When would you use this in research?

Measures of Central tendency

Median

Important

  • The middle number; obtained by ordering all values from lowest to highest and taking the middle (if n is odd or the average of the 2 middle if n is even)

  • \(\large{x = \{4,2,5,6,3\}}\)

  • \(\large{x = \{2,3,4,5,6\}}\)

  • \(\large{x = \{2,3,\color{blue}{4},5,6\}}\)

  • Why is median typically used for income?

  • When would you want this for research?

Measures of Central tendency

Mode

Important

  • The most frequent answer; obtained by counting how many times each answer is given and taking the value that occurs most often

  • \(x = [1,1,2,2,\color{green}{3},\color{green}{3},\color{green}{3},4,5,7,8]\)

  • What’s your favorite genre of music?

  • When would you want this for research?

Measures of Central tendency

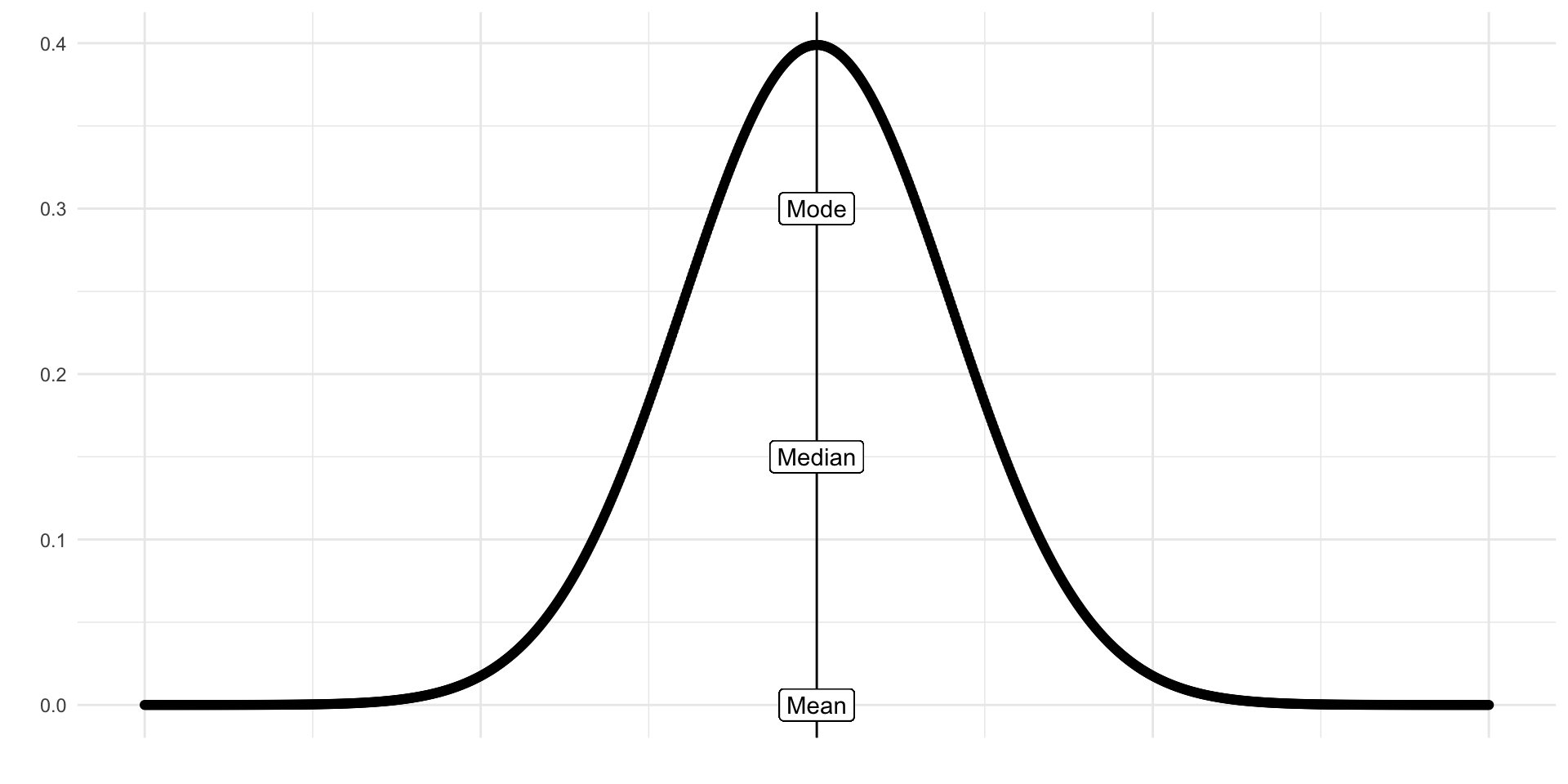
Standard Normal Distribution

In a normal distribution, the mean, median, and mode are equal to one another.

Mean = Median = Mode

Measures of Central Tendency

Mean

  • The mean is only helpful in a normal distribution, which you may have heard called a normal curve or bell curve.

  • We overwhelmingly use the mean, because in the social and behavioral sciences, we nearly always assume the distribution is normal.

Why Do We Assume Normality?

  • We assume normality because the math works better

  • The Central Limit Theorem makes it reasonable

  • Many human traits actually do cluster in bell-shaped patterns.

Central Limit Theorem

The Galton Board

More Examples

Measures of Central tendency

When should we use the median…

  • A skewed distribution occurs when one side of the data gets cut off due to measurement limitation.

  • In a skewed distribution, the mean gets pulled out toward the tail, and the mode gets pulled to the cluster.

  • The median is the best measure of central tendency for skewed distributions because it tells us how most people answered.

Measures of Central tendency

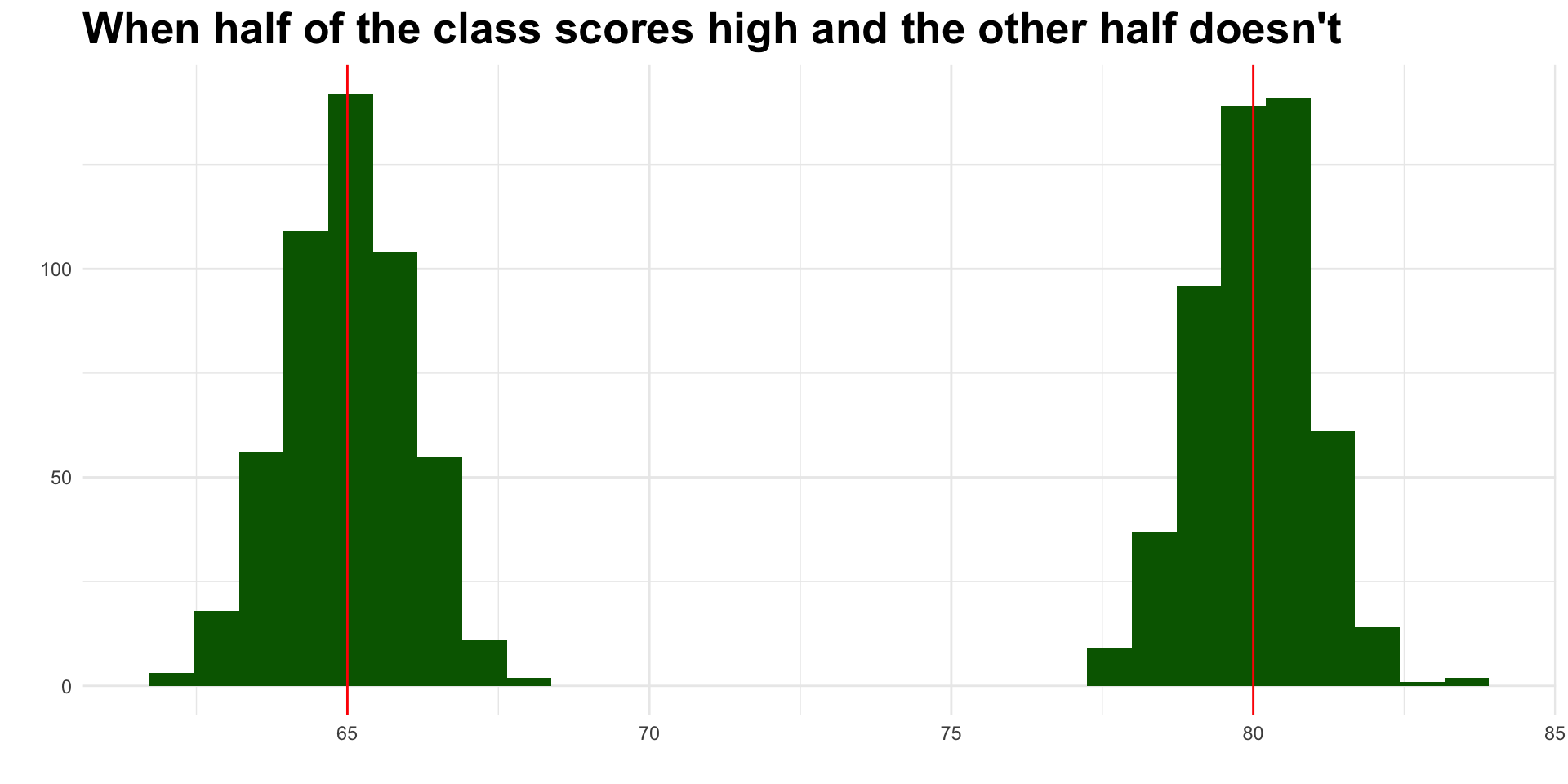
The Mode

  • The mode is good for bi-or-tri-modal distributions.

  • When might you have a bi-modal distribution?

Measures of Central Tendency

Example: Mode

When should we use…

  • Mean

    • good for normal distributions

  • Median

    • good for skewed distributions

  • Mode

    • good for bi-modal distributions

Central Tendency

Which should we use?

Central Tendency

Which should we use?

Central Tendency:

Which should we use?

Calculating measures of central Tendency

Calculating The mean

Tip

  1. Sum all x values
  2. Divide by the number of x values (n).
  3. \(\large{x = 4,2,5,6}\)
  4. \(\large{\frac{\sum(x)}{n}}\)
  5. \(\large{\sum(x) = 4 + 2 + 5 + 6 = 17}\)
  6. \(\large{\frac{17}{4} = \color{red}{4.25}}\)

Calculating measures of central Tendency

Calculating The median

Tip

  1. Put all x values in order from smallest or largest or largest to smallest.
  2. Find the middle number.
  3. If there are an even number of x values, take the average of the 2 middle numbers.
  4. \(\large{x = \{6,2,4,2,8\}}\)
  5. \(\large{x = \{2,2,4,6,8\}}\)
  6. \(\large{x = \{2,2,\color{blue}{4},6,8\}}\)

Calculating measures of central tendency

Calculating The mode

Tip

  1. Put all x values in order from smallest or largest or largest to smallest.
  2. Find the number or numbers that repeat the most.
  3. \(\large{x = [3,2,1,5,3,7,8,3,2,4,1]}\)
  4. \(\large{x = [1,1,2,2,\color{green}{3},\color{green}{3},\color{green}{3},4,5,7,8]}\)
  5. There can be more than 1 mode.

Using Excel

Excel Practice

  • What does each row in this spreadsheet represent?

  • What does each column in this spreadsheet represent?

Excel Practice

  • Adding & Sum: SUM(B2:B10)

  • Subtracting: =C9 - C2

  • Multiplying: =B12 * 4

  • Dividing: =A2/B3

  • Squaring: =(B2-C2)^2

  • Average: =AVERAGE(B2:B20)

Excel Practice

  • Calculate the Mean

  • Using =SUM(x)/n

  • Using =AVERAGE(x)

  • Calculate the Median

  • Find the Mode(s)

Review

When do we use the and how do we caluclate the…

  • Mean?

  • Median?

  • Mode?

Key Takeaways Slide

  • Mean → good for symmetric/normal.

  • Median → good for skewed/outlier-heavy.

  • Mode → good for categorical or multi-modal

  • We assume normality because it lets us use the mean.